왜도(Skewness) 시각화

왜도 시각화

왜도는 데이터 분포 대칭성을 나타내는 지표이다. 데이터가 우측으로 기울어진, 즉 좌측으로 꼬리가 긴 형태는 양수 값을 갖고 그 반대 경우는 음수 값을 갖는다. 왜도 수식은 아래와 같다.

\(\mu_3 = E\left[\left(\frac{(X_i-\mu)}{\sigma}\right)^3\right] = \frac{\sum_i^N(X_i-\mu)^3}{N\times\sigma^3}\)

아래와 같이 데이터를 주어 졌을 때, 왜도 수식을 따라 시각화 해 본다.

data <- c(1,1,2,2,2,3,3,3,3,3,
          4,4,4,4,4,4,4,4,4,4,
          5,5,5,5,5,5,5,5,5,5,5,5,5,
          6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,
          7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,
          8,8,8,8,8,8,8,8,8,8,8,8,
          9,9,9,9,9,9,9)

mu1 <- mean(data)
sigma1 <- sd(data)
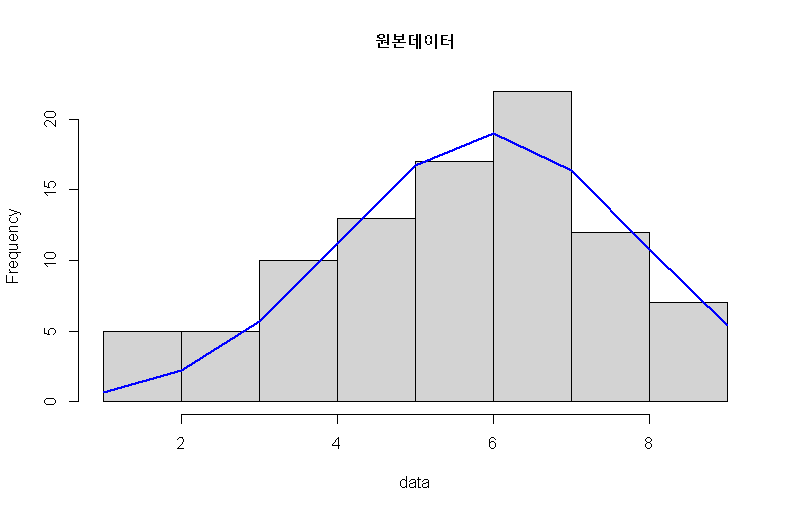
h1 <- hist(data, main = '원본데이터')
xfit1 <- seq(1,9,length=9)
yfit1 <- dnorm(xfit1, mu1, sigma1)
yfit1 <- yfit1*diff(h1$mids[1:2])*length(data)
lines(xfit1, yfit1, col="blue", lwd=2)

원본데이터를 표준화하여 시각화해 본다.

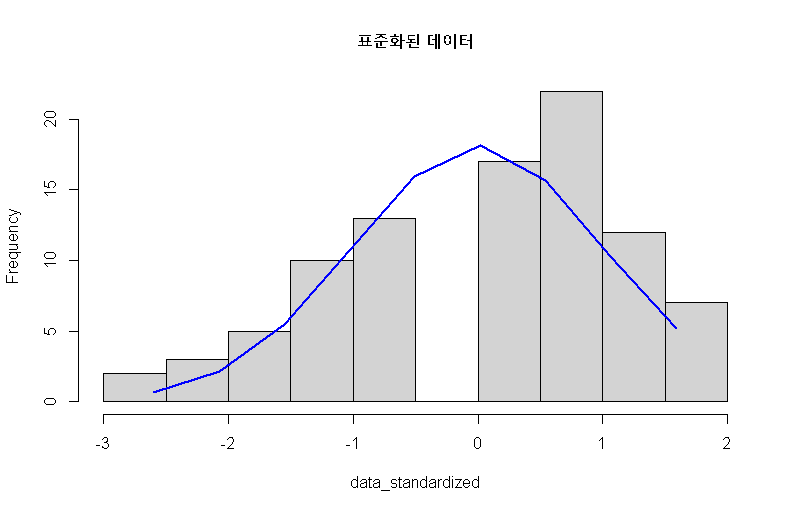
data_standardized <- ((data-mu)/sigma)
mu2 <- mean(data_standardized)
sigma2 <- sd(data_standardized)
h2 <- hist(data_standardized, main="표준화된 데이터")
xfit2 <- seq(min(data_standardized),max(data_standardized),length=9)
yfit2 <- dnorm(xfit2, mu2, sigma2)
yfit2 <- yfit2*diff(h2$mids[1:2])*length(data_standardized)
lines(xfit2, yfit2, col="blue", lwd=2)

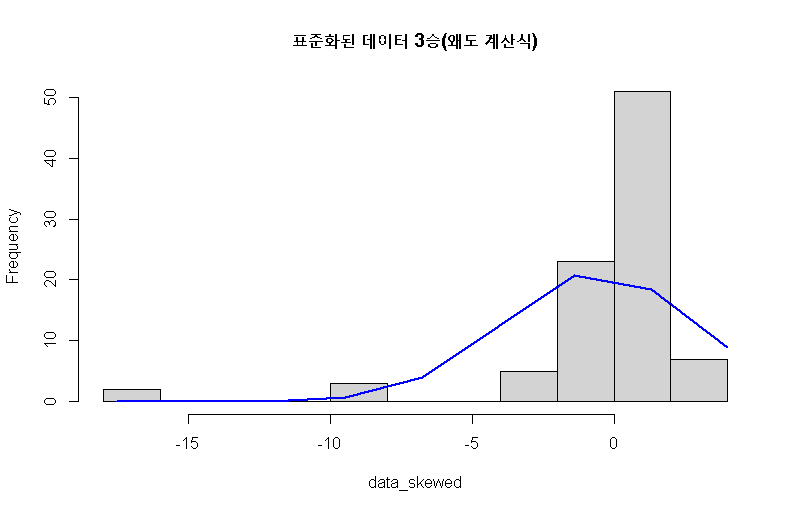
마지막으로 왜도 계산을 위한 수식에 따라 3승을 한 분포를 시각화해 본다.

data_skewed <- ((data-mu)/sigma)^3
mu3 <- mean(data_skewed)
sigma3 <- sd(data_skewed)
h3 <- hist(data_skewed, main="표준화된 데이터 3승(왜도 계산식)")
xfit3 <- seq(min(data_skewed),max(data_skewed),length=9)
yfit3 <- dnorm(xfit3, mu3, sigma3)
yfit3 <- yfit3*diff(h3$mids[1:2])*length(data_skewed)
lines(xfit3, yfit3, col="blue", lwd=2)

실 왜도값을 계산하면 다음과 같다.

# 직접 계산
mean(data_skewed) # [1] -0.5198211

# e1075 패키지
library(e1071)
skewness(data)    # [1] -0.5198211

참고자료

1. https://www.geeksforgeeks.org/skewness-and-kurtosis-in-r-programming/
2. https://www.datacamp.com/doc/r/histograms-and-density