flowchart LR
문제해결 ----- 6 & 7
의사결정 ---- 1 & 2 & 3 & 4 & 5
문제해결 ---- 의사결정
subgraph a2[ ]
1["1.문제를 규명하고 정의한다."]
2[2.여러 문제해결 대안을 결정한다.]
3[3.대안을 평가할 기준을 결정한다.]
4[4.대안을 평가한다.]
5[5.가장 좋은 대안을 선정한다.]
subgraph a1[" "]
6[6.선정된 대안을 실행한다.]
7[7.만족스런 해인지 결과를 평가한다.]
end
end
경영과학
경영과학, OR, 의사결정, 평가안, 문제해결방법, TRIZ, 확실성하, 불확실성하, 위험성하, 상충하
경영과학 이해
경영과학(operations research)은 복잡하고 불확실한 환경에서 발생하는 경영의사결정 문제 분석과 해결을 위하여 합리적이고 체계적인 계량적 방법을 적용한 학문이다.
목적 여러 가지 모델과 기법들을 적용하여 경영자가 직면한 복잡하고 불확실한 경영문제를 합리적이고 체계적으로 해결함으로써 좋은(옳은) 결정을 내릴 수 있도록 도와주는 것
특징
- 경영의사결정을 위한 과학적 방법 사용
- 문제해결을 위한 계량적, 객관적, 수학적 모델(model) 사용
- 문제해결을 위한 분석 도구(tool), 절차(algorithm), 기법(technique) 사용
경영과학은 경영과학(management science), 결정과학(decision science), 계량경영학(quantitative management), OR(operations research), 산업공학(industrial engineering) 등 유사 용어로 사용된다.
경영과학 발전 과정을 정리하면 다음과 같다.
- 1930년대 말 영국 군부에서 군사문제 해결을 위해 학제적 팀 적근법 사용
- 2차 대전 중 미국이 영국의 작전연구(operational research) 모방, 작전분석을 위해 팀 워크 구성
- 1947년, G.Dantzig 선형계획법 개발
- 대형 컴퓨터 개발로 경영 문제를 해결하는 학문분야로 자리 매김
- 2차 대전 이후 산업계에서 OR 기법 적용 시작
- 1960년대 대기행렬이론, 시뮬레이션 모델 개발
- 1970년대 이후 MIS와 결합하여 DSS 탄생
- 전문가 시스템, 인공지능 개발로 발전
경영과학 특성은 다음과 같다. - 경영의사결정에 관심 - 과학적 방법 - 시스템적 접근 방법 - 학제적 팀워크 - 수학적 모델 사용 - 컴퓨터 활용
의사결정과 문제해결
문제해결(problem solving)은 원하는 결과와 실제 결과 사이에 존재하는 차이를 규명하고 이 차이를 해결할 조치를 취하는 과정(process)이다. 의사결정(decision making)은 문제를 정의하고, 대안을 결정하고, 결정 기준을 마련하고, 대안을 선정하는 과정이다.
의사결정 과정에는 질적분석과 수리적 분석이 있다.
질적 분석(qualitative analysis) 대안을 평가할 때 경영자 경험이나 판단력 같은 기예(art)에 의존하는 방법
수리적 분석(quantitative analysis) 대안을 평가할 때 계량적 자료와 수학적 모델 및 기법을 사용하는 방법
경영자는 더 좋은 경영문제 해결을 위해 질적 분석과 수리적 분석을 결합하여 사용한다.
flowchart LR
subgraph g1[문제 구성]
direction LR
문제정의 ---> 대안결정 ---> 기준결정
end
subgraph g2[문제 분석]
기준결정 ---> 질적분석 & 수리적분석 ---> 요약평가 ---> 의사결정
end
과학적 방법
과학적 방법(scientific method)은 17세기 이후 자연과학에 의해 정형화된 계획적 관찰, 측정, 실험, 일반화, 시험 및 가설 변경 등의 과정으로 이루어진 방법을 뜻한다.
과학분야에 따라 과정이 동일일하지는 않으나 현상을 설명하는 가설을 수립하고 이 가설에 의한 예측이 들어 맞는지 검증하기 위해 실험 설계 과정이 반드시 포함된다. 과학적 방법을 통하여 얻은 지식은 경험적이며 귀납적인 것으로 반증 가능성이 언제나 존재한다. 과학 발전에 따라 과학 지식은 그 의미와 내용이 변할 수 있기 때문이다.
과학적 방법 특징은 다음과 같다(F.N. Kerlinger, 1986).
- 문제 해결은 상식적 접근보다 논리적 접근을 통해 이루어진다.
- 이론이나 가설은 체계적이고 경험적으로 검증된다.
- 체계적이고 표준화된 관찰이나 실험은 통제를 통해 이루어진다.
- 사상 체계나 상호관계가 객관성 있고 타당성 있게 설명된다.
- 문제에 대한 연구자 관심 정도에 따라 과학적 방법의 의미가 달라질 수 있다.
flowchart LR
subgraph g1[의사결정과정]
11[문제정의]
12[대안설정]
13[대안평가]
14[의사결정]
end
subgraph g2[과학적방법]
21[문제정의]
22[가설설정]
23[실험 설계와 실행]
24[가설 채택 또는 기각]
end
11 ---> 21
12 ---> 22
13 ---> 23
14 ---> 24
시스템적 접근
경영과학 특성 중 하나는 시스템적 접근 방법이다.
- 시스템
- 특정 목적을 달성하기 위하여 구성되는 상호 관련된, 독립적인 부분(하위 시스템, subsystem)의 전체(모임, 집합)
- 하위 시스템도 시스템
- 시스템적 접근 방법
- 전체 시스템 관점에서 하위 시스템 문제를 해결하는 것
- divide and conquer
- 최적화(optimization)
- 전체 최적화(global optimization) 전체 시스템 목적에 부합하는 해(global optimum)을 찾는 것
- 부분 최적화(sub optimization) 어느 하위 시스템 목적에는 부합하지만 전체 시스템 목적에는 부합하지 못하는 해(local optimum)를 찾는 것
수학적 모델
모델(model, 모형)은 실제 세계 특정 현상이나 실체를 단순하게 요약하여 표현한 것이다. 문제를 기술하고 표현하는 모델화(modelling, 모형화)는 여러 가지 혜택도 주지만 동시에 위함도 따르므로 현실 문제에 대한 통찰력이 필요하다. 또한 모든 모델은 가정을 수반하게 된다.
- 가정(assumption)
- 가정을 세우면 실제 문제 복잡성을 감소시켜 단순화 하는데 도움이 됨
- 단순화 vs. 정확성
좋은 모델이란 모델이 표현하고자 하는 실체 핵심을 문제 해결 관점에서 단순하면서도 정확하게 나타낸 것이다.
모델 종류는 다음과 같다.flowchart LR
0[모델종류]
1["형상모델"]
2["상사모델"]
3["수학적 모델"]
subgraph " "
0 --- 1 & 2 & 3
end
- 형상모델 (iconic model), 또는 축적 모델 (scale model)
- 물리적으로 확대 또는 축소한 원형 복사판
- 장난감, 사진, 생산라인 등
- 상사모델 (analog model)
- 실제 시스템처럼 기능하는 모델
- diagram, 조직표, 청사진, 속도계, 온도계 등
- 수학적 모델 (mathematical model)
- 실제 문제를 수학적 기호를 사용하여 방정식이나 수학적 설명 등을 함수적 관계로 표현한 모델
- 장점
- 문제 이해를 돕는다.
- 다양한 수학적 해결 절차를 적용할 수 있게 해 준다.
- 실행하는 시스템에서 일을 하는 사람에게 해를 만들 수 있도록 도와 준다.
수학적 모델 구성 요소는 다음과 같다.
flowchart LR subgraph sg1["수학적 모델 구성요소"] 구성요소 --- 변수 & 상수 변수 --- 독립변수 & 종속변수 독립변수 --- 결정변수 & 외생변수 end
수학적 모델에서는 구성요소로 변수와 상수가 있으며 자세한 내용은 다음과 같다.
- 변수(variable)
- 시간이나 조건에 따라 값이 변할 수 있는 것
- 독립변수(independent variable)
- 다른 변수에 영향을 받지 않는 변수
- 결정변수(decision variable), 통제가능변수(controllable variable) - 의사결정자가 자의적으로 변경할 수 있는 변수 - 총비용, 총수입 등
- 외생변수(exogenous variable), 통제불가능변수(uncontrollable variable) - 의사결정자가 자의적으로 통제할 수 없어 주어지는 대로 받아 들이는 변수 - 이자율, 사망률, 경쟁제품 가격 등
- 종속변수(dependent variable), 기준변수(criterion variable)
- 독립변수 값에 영향을 받는 변수
- 총이익
- 상수(constant), 매개변수(parameter)
- 시간이나 조건에 따라 변하지 않고 고정된 값
- 원주율, 자연로그 등
수학적 모델 분류는 다음과 같다.
flowchart LR
subgraph " "
0[수학적 모델]
subgraph g1[" "]
11[규범적 모델]
12[서술적 모델]
end
subgraph g2[" "]
21[확정적 모델]
22[확률적 모델]
end
subgraph g3[" "]
31[분석적 모델]
32[시뮬레이션 모델]
end
0 --- g1 & g2 & g3
end
수학적 모델별 내용은 다음과 같다.
- 규범적 모델과 서술적 모델
- 규범적 모델 (normative model), 최적화 모델 (optimization model)
- 의사결정자가 특정 목적을 가장 효율적으로 달성하기 위해서 취해야 하는 행위를 규정(prescribe)하는 모델
- 규범적 모델은 최적해 (optimal solution)를 구하기 위하여 사용
- 선형계획법, 네트워크 모델, 수송 모델, 동적 계획법 등
- 서술적 모델 (descriptive model)
- 의사결정이 실제로 어떻게 이루어지는가를 기술(describe)하는 모델
- 여러 대안 결과, 즉 시스템 성과 또는 효과성을 조사하기 위하여 사용하며, 만족해(satisficing solution)를 제공함
- 대기행렬, 마이코브 분석, 시뮬레이션 모델 등
- 규범적 모델 (normative model), 최적화 모델 (optimization model)
- 확정적 모델과 확률적 모델
- 확정적 모델 (deterministic model)
- 통제불능변수 값을 사전에 확실히 알고 사용하는 모델
- 선형계획법, 수송모델 등
- 확률적 모델 (probabilistic model)
- 통제불능변수 값이 불확실하고 변동하는 경우에 사용하는 모델
- 재고관리 모델, 대기행렬 모델, 시뮬레이션 모델 등
- 확정적 모델 (deterministic model)
- 분석적 모델과 시뮬레이션 모델
- 분석적 모델 (analytic model)
- 반복적 연산절차나 일반해 공식을 사용하는 모델
- 선형계획법, 재고관리 모델 등
- 시뮬레이션 모델 (simulation model)
- 해가 연역적으로 구해지는 것이 아니고 어떤 조건 하에서 모델에 통제가능한 변수 특정값을 대입하여 종속변수에 미치는 영향을 관찰찰함으로써 실험하는 모델
- 슈퍼마켓 계산대 수가 고객 도착률에 따라 총비용에 미치는 영향 실험 등등
- 분석적 모델 (analytic model)
의사결정 도구
의사결정 도구는 불확실성 하에서 미래를 예측하거나 여러 가지 대안을 평가하거나 상호 영향에서 최선의 선택을 도와준다.
flowchart TD
0[의사결정 도구]
subgraph s1[불확실성 하 미래예측]
direction LR
11[의사결정론]
12[의사결정나무]
13[몬테카를로 시뮬레이션]
14[마코프 체인 분석]
end
subgraph s2[여러 가지 대안 평가]
direction LR
21[손인분기점 평가]
22[선호도 행렬]
23[선형/비선형 계획법]
24[AHP/ANP]
end
subgraph s3[상호 영향]
direction LR
31[게임이론]
s32["투명노드"]
s33["투명노드"]
s34["투명노드"]
end
0 --> s1 & s2 & s3
%% 스타일
style s1 fill:#f9f9f9
style s2 fill:#f9f9f9
style s3 fill:#f9f9f9
%% 숨기고 싶은 노드: 공간은 유지하되 표시 안 함
style s32 fill:none,stroke:none,color:#fff,opacity:0
style s33 fill:none,stroke:none,color:#fff,opacity:0
style s34 fill:none,stroke:none,color:#fff,opacity:0
의사결정 환경
의사결정 환경은 크게 확실성하, 위험하, 불확실성하 그리고 상충하에서의 의사결정이 있다.
flowchart TD
00[의사결정 환경]
subgraph s10[확실성하 의사결정]
direction LR
선형계획법
수송법
할당법
동적계획법
s11[투명노드]
style s11 fill:transparent,stroke:none,color:#fff,opacity:0
end
subgraph s20[위험하 의사결정]
direction LR
s29[PERT/CPM]
대기행렬이론
시뮬레이션
마크브연쇄모형
s21[투명노드]
style s21 fill:transparent,stroke:none,color:#fff,opacity:0
end
subgraph s30[불확실성하 의사결정]
direction LR
맥시맥스준거
맥시민준거
후르비치준거
유감준거
라플라스준거
end
subgraph s40[상충하 의사결정]
direction LR
게임이론
s41["투명노드"]
s42["투명노드"]
s43["투명노드"]
s44["투명노드"]
style s41 fill:transparent,stroke:none,color:#fff,opacity:0
style s42 fill:transparent,stroke:none,color:#fff,opacity:0
style s43 fill:transparent,stroke:none,color:#fff,opacity:0
style s44 fill:transparent,stroke:none,color:#fff,opacity:0
end
00 --> s10 & s20 & s30 & s40
- 확실성하 의사결정
- 대안을 선택할 때 어떤한 상황이 발생할 것인지를 확실하게 알고 있는 경우
- 고전적 최적화 기법, 손익분기점분석, 선형계획법, 비선형계획법, 수송법, 할당법(배정법), 목표 계획법, 정수계획법, 동적계획법 등
- 위험하 의사결정
- 대안을 선택할 때 상황 발생 여부를 확률적으로 알고 있는 경우
- 사전정보를 이용한 의사결정, 의사결정, 재고모형이론
- 사전정보와 표본정보를 이용한 의사결정, PERT/CPM, 대기행렬이론, 시뮬레이션, 마코브연쇄모형 등
- 불확실성하 의사결정
- 대안을 선택할 때 상황발생 확률을 전혀 모르는 경우
- 라플라스 준거, 맥시맥스 준거, 맥시민 준거, 후르비츠 준거, 유감 준거
- 상충하 의사결정
- 서로 상충적인 이해관계를 가진 의사결정자들이 상대방에 대응하여 의사결정을 하게 되는 경우(게임모형, Game Mode)
- 게임이론
불확실성하 의사결정
불확실성하 의사결정은 어떠한 사건에 대해 과거 경험이 전무하여 발생 가능확률이 알려지지 않아거나 미래에 대한 확실한 근거를 가지고 예측하기 매우 어려운 경우에 이루어지는 의사결정으로 경영활동 상 대부분이 이 경우에 해당된다.
의사결정론
의사결정론에 있어 의사결정이란 무엇을 어떻게 결정해야 하느냐에 대한 물음에 답하는 것으로 의사결정자가 선택할 행위가 복수개여야 한다. 참고로, 관리 불가능 변수란 의사 결정권자 결정과는 관계없이 의사결정 결과에 영향을 주는 요소를 의미한다.
불확실한 상황 하에서의 의사결정은 선택 가능한 대안, 발생 가능성, 여러 상황에 있어 각 대안들 간 수익성 그리고 알려지지 않은 여러 상황들의 발생 확률 속에서 의사결정자 성향이나 의사결정 상황에 따라 기준이 마련된다.
- 최대최소(Maximin, Wald) 기준
- 비관적인 관점에서 미래 수요가 낮은 것을 선택
- 미래에 대해 비관적인 예측에 준해 의사결정한 최악의 대안 중 가장 좋은 결과를 보상해 주는 대안을 선택
- 안전제일 주장으로 각 상황별로 손실이 가장 작은 경우를 의사결정 기준으로 삼음
- 최대최대(Maximax) 기준
- 최대로 낙관적인 수익을 예상하며 미래 수요가 높은 것을 선택
- 미래에 대해 낙관적인 예측에 준해 의사결정한 최상의 대안 중 가장 좋은 결과를 보상해 주는 대안을 선택
- 라플라스(Laplace) 기준
- 가중평균 보상이 가장 좋은 것을 선택
- 미래를 정확히 예측할 수 없기 때문에 모든 상황이 동일한 확률로 발생한다는 가정(사건이 n가지일 경우 각 사건 비중은 1/n 임)하에 각 대안별로 기댓값을 계산하여 가장 좋은 값을 갖는 대안을 선택
- “불충분 이유 원칙”이라고 하며 각 상황에 따른 평균을 의사결정 기준으로 삼음
- 최소최대후회(Minimax Regret, 세비지 Savage) 기준
- 최악의 후회(최소 투자를 하였는데 수요가 많은 경우)가 가장 작은 대안을 선택
- 최대후회 최소화(minimax, savage) 원칙은 의사결정자가 자기 행동 결과를 후회하지 않으려 하며 적어도 의사결정에서 오는 최대 후회를 최소화 하려고 하는 가정에 근거
- 결과표를 후회표(주어진 사건 하에서 최선 대안안인 최대치에서 해당 값을 빼주어 얼마나 손해 보는가를 나타냄)로 전환하여 그 중 가장 작은 값을 가지는 대안 선택
- 후르비치(Huwicz) 기준
- 최대최대원책과 최대최소원칙의 가중평균
- 대부분 의사결정자는 현실적으로 극단적으로 비관적 또는 낙관적 기준이 아닌 중간 어느 지점을 선택함
- 비관주의와 낙관주의를 절충하기 위해서 의사결정자가 으느 정도 미래에 대한 낙관적인 견해를 가지고 있는 정도를 나타내는 낙관지수(\(\alpha\))를 가중치로 사용하며 이 지수는 0 ~ 1 사이 값을 가지고 낙관지수가 0일 때는 의사결정자가 자연 결과에 대해 비관적(최대최소원칙)이며, 반면 1일 때는 자연에 대낙관적(최대최대)이라는 것을 의미함
의사결정 나무
의사결정 나무(decision tree) 기법은 의사결정이 단계별로 연속적으로 이루어지는 경우에 사용할 수 있는 분석 기법으로 1964년 매기(J.F. Magee)에 의해 제기되었다. 생산규모 확장 시기 결정에 이용되는 확률적 기법으로 의사결정에서 고려되는 대체안 구조를 여러 갈래 가지와 마디를 작고 있는 나무 모양으로 나타낸 방식이다.
수요가 불확실하고 순차적으로 여러 의사결정을 내려야 하는 다양한 경우를 평가하는데 유용하다.
의사결정나무 작성방법은 다음과 같다.
아래 기호를 이용하여 도식화 한다.
(□) 사각형 결정 마디
어떤 결정이 필요한 상태를 나타내는 의사결정 지점(○) 원형 사건 마디
의사결정 선택과 상황 간 결과를 설명하는 상황 발생점(ㅡ) 가지
의사결정 또는 상황 발생점에서 뻗어 나온 가지로 의사결정 대안을 표시하기도 하고 선택과 상황이 이루어질 때 다양한 결과를 의미하기도 함
의사결정 나무 작성 작성 절차는 다음과 같다.
- 사건 마디에 대해 각 사건 가지 보상과 확률을 곱하고 이들을 모두 더하여 사건 마디 기대 보상을 계산
- 상황 발생점에서는 상황 발생점에서 뻗은 가지에 있는 미래상황 발생 확률과 성과를 곱한 결과 합을 기입하고 이를 위치 값이라하며 상황 발생점 왼쪽에서 빧어 나온 가지의 성과가 됨
- 결정 마디에선 기대 보상이 가장 높은 대안을 선택
- 의사결정 시 각 대안 위치 값을 비교하여최선 대안을 선택하여 기입
위험하 의사결정
위험하 의사결정 도구로는 시뮬레이션과 대기행렬이론 등이 있다.
시뮬레이션
시뮬레이션이란 최적해를 도출하는 기법이라기보다 어떤 실제 현상을 모형화하여 제작한 후 그 모형에 대한 실험을 수행함으로써 관계되는 결과치를 도출하고 이를 실제 현상에 적용하기 위한 방법이다. 시뮬레이션을 사용하는 이유는 실제 상황에 대한 실험이 비실용적이거나 불가능할 경우, 수학적인 표현이나 모델 해를 제시하기에 실제 상황이 너무 복잡할 경우에 사용하게 된다.
시뮬레이션 의의는 다음과 같다.
- 비용 절감 및 리스크 최소화
실제 생산 시스템을 변경하거나 실험하는 대신 시뮬레이션을 사용하여 다양한 상황을 미리 실험할 수 있다. 이를 통해 실험에 필요한 비용이나 리스크를 줄일 수 있다. - 의사결정 지원
시뮬레이션은 다양한 시나리오를 모델링하여 각 시나리오의 결과를 예측할 수 있기 때문에, 관리자는 시뮬레이션 결과를 바탕으로 보다 효과적인 의사결정을 내릴 수 있다. - 효율성 향상
생산 공정에서 발생할 수 있는 병목 현상이나 자원의 불균형 등을 사전에 파악하여 최적화할 수 있다. 이를 통해 생산 효율성을 높이는 데 기여한다.
- 시스템 이해 시뮬레이션을 통해 복잡한 생산 시스템을 더 잘 이해하고, 각 구성 요소가 어떻게 상호작용하는지 파악할 수 있다. 이는 시스템 개선을 위한 중요한 통찰을 제공한다.
시뮬레이션 장점은 다음과 같다.
- 위험 없이 실험 가능
실제 생산 환경에서 발생할 수 있는 위험을 피하면서 시스템을 시험하고 실험할 수 있다. 예를 들어, 생산 라인을 멈추지 않고도 새로운 공정이나 변화의 영향을 테스트할 수 있다. - 시간과 공간 절약
실험을 실제로 진행하는 것보다 빠르고 효율적으로 결과를 도출할 수 있. 또한, 물리적인 공간이나 리소스를 사용하지 않으므로 시간과 비용을 절감할 수 있다. - 다양한 변수 실험 가능
시뮬레이션을 통해 다양한 변수나 조건을 변경하면서 그 영향을 쉽게 분석할 수 있다. 이는 실제 환경에서 실험하기 어려운 변수들을 포함할 수 있는 장점이 있다. - 시나리오 비교
여러 가지 시나리오를 동시에 비교하여 최적의 운영 방안을 도출할 수 있다. 예를 들어, 다른 생산 일정이나 자원 배분 방식을 비교하여 가장 효율적인 방법을 선택할 수 있다.
이에 반해 다음과 같은 단점을 갖는다.
- 모델링의 정확성 문제
시뮬레이션은 실제 시스템을 모델링한 결과이기 때문에 모델이 정확하지 않으면 시뮬레이션 결과도 신뢰할 수 없다. 시스템의 복잡성이 클수록 정확한 모델링이 어려워질 수 있다. - 고도의 전문성 요구
시뮬레이션을 효과적으로 사용하려면 관련 도구와 기술에 대한 높은 수준의 이해와 전문성이 필요하다. 잘못된 설정이나 이해로 인해 잘못된 결론을 도출할 위험이 있다. - 실제 환경과의 차이
시뮬레이션은 현실을 그대로 반영하는 것이 아니므로, 실제 환경에서 발생할 수 있는 예기치 않은 변수나 상호작용을 완벽하게 재현하는 데 한계가 있을 수 있다. - 비용과 시간
시뮬레이션 시스템을 구축하고 운영하는 데 시간이 오래 걸리고 비용이 들 수 있다. 특히, 복잡한 시스템이나 정확한 모델링을 요구하는 경우 더 많은 자원이 소모된다.
결론적으로, 생산 시스템에 시뮬레이션을 적용하면 여러 이점을 제공하지만, 그 효용성을 최대화하려면 정확한 모델링과 적절한 해석이 필요하다.
대기행렬이론
대기행렬이론(Queueing Theory)은 고객과 서비스 시설 간 관계를 확률 이론을 적용하여 모형을 작성하고 고객 도착 상황에 대응할 수 있는 경제적 규모를 결정하고자 하는 의사결정 기법이다. 총 대기 비용을 최소화시키는 최적 서비스 시설 결정을 위한 기법으로 대기행렬 분석에 따라 프로세스 설계, 용량 계획, 프로세스 성과가 달라지게 된다. 다음과 같은 경우 대기행렬이 생기거나 서비스 시설이 휴지상태에 이르게 된다.
- 불규칙한 고객 요구(도착)
- 서비스 능력 크기
- 수요와 서비스 시스템 간 일시적인 불균형
대기행렬 현상은 다음과 같다.
- 은행이나 병원에서 차례를 기다리는 고객
- 생산 공장에서 수리를 기다리는 고장 난 기계
- 재료나 일감 공급을 기다리는 작업공정
대기행렬 분석 목적은 고객 도착 상황에 잘 대응할 수 있는 능력 내지 규모를 경제적으로 결정하여 서비스 비용을 최소화 하는데 있다.
일반적인 대기행렬 시스템 기본 구조는 다음과 같다.
| 구성 요소 | 설명 | 예시 |
|---|---|---|
| 고객 (Customer) | 서비스를 받기 위해 대기행렬에 도착하는 개체 (사람, 기계, 작업 등) | 은행 고객, 고장 난 기계, 처리해야 할 주문 |
| 도착 과정 (Arrival Process) | 고객이 대기행렬에 도착하는 패턴 | 일정한 간격으로 도착, 무작위로 도착 (포아송 분포), 그룹으로 도착 |
| 대기행렬 용량 (Queue Capacity) | 대기행렬이 수용할 수 있는 최대 고객 수 | 무한대, 제한된 좌석 수, 버퍼 크기 |
| 대기 규율 (Queue Discipline) | 대기하고 있는 고객이 서비스를 받는 순서 규칙 | 선착순 (FIFO), 후착순 (LIFO), 우선순위, 무작위 |
| 서비스 시설 (Service Facility) | 고객에게 서비스를 제공하는 주체 (창구, 수리공, 처리 장치 등) | 은행 창구, 병원 진료실, 컴퓨터 서버 |
| 서비스 과정 (Service Process) | 서비스 시설이 고객에게 서비스를 제공하는 데 걸리는 시간 패턴 | 일정한 서비스 시간, 확률 분포를 따르는 서비스 시간 (지수 분포) |
| 서비스 채널 수 (Number of Service Channels) | 동시에 서비스를 제공할 수 있는 서비스 시설의 수 | 단일 서버 (은행 창구 1개), 다중 서버 (은행 창구 여러 개) |
대기행렬 가정
대기행렬 이론 가정은 다음과 같다.
- 고객 수 분포
- 시간당 고객 도착 수는 포아송 분포를 따른다.
- 서비스 시간 분포
- 고객이 도착하는 시간 간격은 지수 분포를 따른다.
단일경로 단일과정 대기행렬 시스템일 경우 대기행렬 평균 길이는 다음과 같이 계산된다.
\[ 대기행렬 \ 평균길이 \ L_q \ = \ \frac{\lambda^2}{\mu(\mu - \lambda)} \tag{29.1}\]
여기서 \(\lambda\)는 단위시간 동안 도착하는 평균 고객 수이고, \(\mu\)는 단위시간 동안 서버 1명에게 서비스를 제공받는 평균 고객 수이다.
대기행렬 모형
- M/M/1
- M: 고객도착 시간 간격으로 포아송 분포를 따른다.
- M: 서비스 시간 간격으로 지수 분포를 따른다.
- 1: 단일경로 단일과정 시스템으로 서비스 시설은 하나다.
확실성하 의사결정
선형계획법
확실성 하에서의 의사결정 모델 중 하나인 선형 계획법(Linear Programming, LP)은 제한된 자원을 효율적으로 배분하여 목표함수(Objective Function) 를 최대화하거나 최소화하는 수학적 기법이다. 확실성이란, 모든 변수(자원, 수요, 비용 등)가 명확하게 알려져 있으며, 변화하지 않는 상황을 의미한다.
- 수리계획법(mathematical programming)
- 의사결정자가 실현하고자 하는 목적을 최적화(최대화 또는 최소화)하고자 문제를 모델화해서 그 해결 절차에 따라 최적해를 찾아내려는 과정
- programming은 계획한다(planning) 또는 최적화 한다(optimizing)를 의미
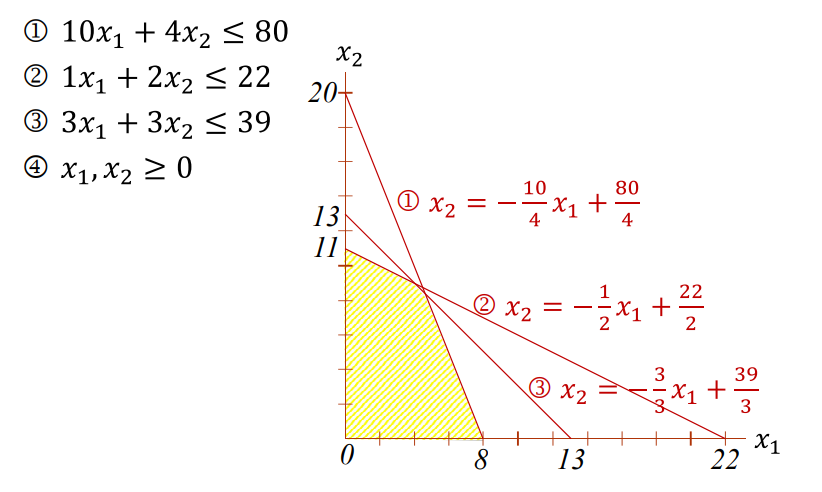
일반적인 선형계획 모델 구조는 다음과 같다.
| 구성 요소 | 설명 |
|---|---|
| 목표함수(Objective Function) | 극대화(이익, 생산량 등) 또는 극소화(비용 등)하려는 함수 |
| 의사결정 변수(Decision Variables) | 결정하고자 하는 변수 (예: 생산 수량 \(x_1, x_2\)) |
| 제약조건(Constraints) | 자원, 시간, 용량 등 현실적인 한계를 수학적으로 표현한 식 |
| 비음 조건(Non-negativity) | 변수는 음수가 될 수 없다는 조건 (\(x_i \ge 0\)) |
\[ \begin{align} max/min \ Z = C_1x_1 + C_2x_2 + ... + C_nx_n \end{align} \tag{29.3}\]
\[ \begin{align} \\subject \ to \\ a_{11}x_1 \ + \ a_{12}x_2 \ + \ ... \ a_{1_n}x_n \ \le \ b_1 \\ a_{21}x_1 \ + \ a_{22}x_2 \ + \ ... \ a_{2_n}x_n \ \le \ b_2 \\ ... \\ a_{m1}x_1 \ + \ a_{m2}x_2 \ + \ ... \ a_{m_n}x_n \ \le \ b_m \\ \end{align} \tag{29.4}\]
\[ \begin{align} where \ x_1 \ge 0, \ x_2 \ge 0, \ , \ ... \ , \ x_n \ge 0 \end{align} \tag{29.5}\]
일반 구조 구성요소는 다음과 같다.
- 결정변수(decision variable)
- \(x_1, x_2, ..., x_n\)
- 기업이 수행하는 활동 수준을 나타내는 기호
- 제품 1 생산량, 제품 2 생산량 등
- 아직 알지 못하는 변수 양을 나타내는 기호
- 목적함수(objective function)
- 위 수식 (29.3)
- 의사결정자가 달성하고자 하는 목적을 최대화(maximize) 또는 최소화(minimize)하려는 선형 함수식
- 최대화: 이익, 수입, 시장점유율, 투자수익 등
- 최소화: 비용, 시간, 거리 등
- 제약조건(constraint)
- 매개변수
- 계수(coefficient)
- 목적함수 계수(objective function coefficient): \(C_1, C_2, ..., C_n\)
- 기술 계수(technology coefficient), 투입-산출계수(input-output coefficient): \(a_{11}, a_{12}, ..., a_{mn}\)
- 우변상수(right hand side value): \(b_1, b_2, ..., b_m\)
- 계수(coefficient)
선형계획법(Linear Programming, LP)은 최적화 문제를 해결하는 수학적 방법으로, 주로 자원 배분이나 의사결정에 있어 최적의 해를 구하는 데 사용된다. 이 방법은 목표 함수와 제약 조건이 모두 선형인 경우에 적용된다. 선형계획법은 다양한 분야에서 효과적으로 활용되고 있다.
- 산업 생산 계획
- 선형계획법은 제조업에서 자원 할당, 생산 계획, 재고 관리 등 최적화 문제를 해결하는 데 사용된다.
- 예를 들어, 다양한 제품을 생산하는 공장에서 각 제품을 위한 원자재 사용량, 생산 시간, 인력 배분 등을 고려하여 생산 계획을 최적화할 수 있다.
- 운송 및 물류
- 물류 네트워크 최적화: 제품을 제조지에서 소비지로 이동시키는 과정에서 운송비용 최소화를 목표로 한다.
- 창고 관리: 여러 창고와 배급처에서 제품을 효율적으로 분배하여 운송 비용을 줄이는 문제를 해결한다.
- 금융 및 투자 관리
- 포트폴리오 최적화: 주식, 채권 등 다양한 금융 자산을 조합하여 위험을 최소화하고, 수익을 최대화하는 포트폴리오를 구성한다.
- 자산 배분: 투자 가능한 자금을 여러 투자처에 분배하여 리스크를 관리하고 최적의 수익을 추구한다.
- 인적 자원 관리
- 인력 배치: 각 직무나 프로젝트에 대해 필요한 인력을 최적의 방법으로 배치하여 인건비 절감과 업무 효율성 향상을 도모한다.
- 근로 시간 관리: 노동 시간이나 인력 배치 최적화를 통해 생산성 향상 및 비용 절감을 추구한다.
- 농업
- 농작물 재배 계획: 다양한 농작물을 재배할 때, 토지 면적, 비료 사용량, 노동력 등의 자원을 고려하여 최적의 재배 계획을 수립한다.
- 수확량 최적화: 농업 자원을 효율적으로 배분하여 생산성을 극대화하는 데 사용된다.
- 에너지 관리
- 전력 생산 및 분배: 여러 발전소에서 생산된 전기를 효율적으로 배분하여 에너지 비용을 최소화하고 안정적인 공급을 보장한다.
- 자원 최적화: 다양한 에너지 자원을 활용하여 최적의 생산 계획을 세우고 비용을 절감한다.
- 서비스 운영 최적화
- 병원 스케줄링: 의료 인력과 장비를 효율적으로 배치하여 병원의 운영 효율성을 극대화한다.
- 호텔 예약 시스템: 객실 예약을 최적화하여 수익을 극대화하는 문제에 적용된다.
- 마케팅 및 광고
- 광고 예산 최적화: 다양한 매체를 활용하여 광고 예산을 효율적으로 분배하고 목표 시장에 맞는 광고 전략을 수립한다.
- 판매 전략: 제품이나 서비스의 가격, 프로모션, 판매 채널을 최적화하여 매출 증대를 도모한다.
선형계획법은 다양한 분야에서 자원의 효율적인 배분을 위해 사용된다. 산업 생산, 물류, 금융 등 많은 분야에서 최적의 해결책을 제공하며, 비용 절감, 수익 증대, 효율적인 자원 관리를 위해 널리 활용된다.
대안평가
AHP
AHP(Analytic Hierarchy Process, 계층 분석법)는 복잡한 의사결정 문제를 구조화하고 정량적으로 분석할 수 있도록 도와주는 다기준 의사결정(Multi-Criteria Decision Making, MCDM) 기법이다. 1970년대에 토마스 사아티(Thomas Saaty)가 개발하였으며, 정성적 요소를 수치화할 수 있다는 점에서 다양한 분야에서 폭넓게 사용된다.
AHP 특징은 다음과 같다.
| 항목 | 설명 |
|---|---|
| 목적 | 여러 대안 중에서 우선순위를 도출하거나 최적 대안을 선택 |
| 구조 | 계층 구조로 의사결정 문제를 분해 |
| 비교 방식 | 쌍대비교(Pairwise Comparison)를 통해 상대적 중요도를 정량화 |
| 산출 결과 | 각 대안의 가중치 및 우선순위, 일관성 지수(CI) |
AHP 원리
인간이 의사결정 시 두뇌가 단계적 또는 위계적 분석 과정을 활용한다는 사실에 착안하여 개발되었다. 연구 결과에 따르면 사람은 문제를 해결할 때 다음 세가지 원칙을 따른다.
- 계층적(hierarchy) 구조 설정
- 상대적 중요도(weight) 설정
- 논리적 일관성 (logical consistency) 유지
계층적 구조 설정
인간은 복작한 현상을 그 구성요소 별로 나아가 더 작은 부분으로 나누어 종국적으로 계층 구조를 설정한다. 가장 기본적으로 맨 윗부분은 목적(goal)을 두고, 그 밑에 판단기준이 되는 기준(criteria)을, 그리고 가장 아래 계층에 대안(alternatives)을 두는 구조이다. 판단기준은 분석 대상에 따라 하위 계층을 두어 복잡한 구조를 가질 수도 있다.상대적 중요도 설정
인간은 관측한 사물 사이의 관계를 인식하고 유사한 사물들을 짝으로 묶어 특정 기준에 대하여 비교하고 그 짝의 구성 인자 사이의 선호도를 판단하는 능력을 소유하고 있다. 최종적으로 상상이나 논리적 과정을 통하여 그들이 내린 판단을 종합하여 전체 시스템에 대한 이해를 보다 강화한다. AHP 특징은 많은 의사결정 요소 간 가중치 또는 중요도(weight)를 간단한 쌍대비교(1:1)를 통해 산출해 내는데 있다.논리적 일관성 유지
인간은 사물이나 생각을 논리적 일관성을 갖도록 관계를 설정하는 능력을 갖고 있다. 일관성은 두 가지 의미를 갖는데 유사한 사물이나 생각을 동질성이나 관련성에 따라 묶는 것과 특정한 기준이 있을 경우 생각이나 사물 간 강약을 기준에 따라 논리적인 방법으로 구성한다는 것이다.
4가지 공리
기본적인 4가지 공리는 다음과 같다.
flowchart LR
subgraph " "
가[4가지 공리]
가 --- 나0[상호비교] & 나1[동질성] & 나2[독립성] & 나3[기대성]
end
상호비교(reciprocal comparison)
의사결정자의 두 대상에 대한 상호 비교가 반드시 가능해야 하며 중요성 정도를 나타낼 수 있어야 한다. 이 중요성 정도는 반드시 역조건을 성립시켜야 한다. 즉 A가 B보다 x배 중요하다면 B는 A보다 (1/x)배 중요시되어야 한다.동질성(homogeneity)
중요성 정도는 한정된 범위 내 정해진 척도를 통해 표현되어야 한다. 즉 비교대상 간 비교 가능한 일정한 범위를 갖는 기준들이 존재해야 한다.독립성(independence)
상대적 중요도를 평가하는 동일 수준 요인들은 특성이나 내용 측면에서 서로 관련성이 없어야 한다.기대성(expectation)
계층구조는 의사결정에 필요한 모든 사항들을 완전하게 포함하는 것을 가정한다. 즉 의사결정자의 합리적 기대에 부합하는 완전한 계층구조를 갖고 있어야 한다. 반면 수준 수가 많아 계층 구조가 깊으면 계산상 복잡성을 유발시키므로 일반적으로 3-7 수준으로 계층을 형성한다.
각 공리는 이론적 또는 실제 이용 측면에서 타당성을 가지기 위해 필요하다. 그 근거는 다음과 같다.
상호비교 위배는 모호한 질문 때문에 의사결장가 질문을 이해하지 못하는 경우 발생한다. 판단이나 상대비교를 이끌어 내는데 사용되는 질문이 명백하지 않거나 질문이 올바르게 언급되지 않았다면 쌍대비교가 성립될 수 없다는 것을 의미한다.
동질성을 만족하지 못한다면 비교되는 요소는 동일하지 못하게 되어 쌍대비교가 성립할 수 없다. 즉, 동질성이란 비교 대상들이 비교 가능하다는 것을 의미한다.
독립성은 판단 기준 가중치가 고려되는 대안들과 독립적이어야 한다는 의미이다. 특정 대안 선택에 유리한 가중치 산출을 피애야 하며 두 기준을 쌍대비교할 때 상위 수준 요소만을 고려해야 한다.
기대성을 만족하지 못한다면 의사결정자는 자신의 합리적 기대를 맞추는데 필요한 모든 대안이나 모든 판단기준을 사용하지 않는 것이다. 즉, 의사결정이 불완전하게 이루어져 기대를 반영하지 못하게 된다.
분석 과정
AHP 분석은 다음과 같은 가정을 따른다.
- 문제설정 및 계층적 구조화
- 문제별 쌍대비교 단계
- 가중치 산정 및 일치성 분석
flowchart TB
subgraph 목표
0[스마트폰 구입]
end
subgraph 평가기준
11[디자인]
12[가격]
13[성능]
14[서비스]
end
subgraph 대안
21[삼성]
22[샤오미]
23[애플]
end
0 --- 11 & 12 & 13 & 14
11 --- 21 & 22 & 23
12 --- 21 & 22 & 23
13 --- 21 & 22 & 23
14 --- 21 & 22 & 23
ANP
ANP(Analytic Network Process, 분석 네트워크 과정)는 AHP(Analytic Hierarchy Process)의 한계를 극복하기 위해 토마스 사아티(Saaty)가 확장한 의사결정 기법이다. AHP가 계층적 구조(Hierarchy)를 가정하는 반면, ANP는 요소 간 상호의존성(Interdependence)을 허용하는 네트워크 구조(Network)를 기반으로 한다.
| 항목 | 설명 |
|---|---|
| 목적 | 상호 의존적 관계가 있는 복잡한 의사결정 문제 해결 |
| 기본 원리 | AHP의 쌍대비교 및 고유벡터 방식 활용 |
| 특징 | 요소들 간의 피드백과 상호작용을 고려 |
| 구조 | 계층(Hierarchy)이 아닌 네트워크 구조(Network) 기반 |
AHP와 ANP를 비교하면 다음과 같이 정리할 수 있다.
| 구분 | AHP | ANP |
|---|---|---|
| 구조 | 계층적(Hierarchical) | 네트워크(Networked) |
| 요소 간 관계 | 독립적 | 상호의존적(Feedback 포함) |
| 적용 범위 | 단순 문제 | 복잡한 상호작용 문제 |
| 계산 방식 | 쌍대비교 → 가중치 | 쌍대비교 → 슈퍼매트릭스 이용 |
다음은 ANP 장점이다.
| 장점 | 설명 |
|---|---|
| 현실 반영력 향상 | 상호의존 관계, 피드백 반영 가능 |
| 정성적 요소 수치화 | 사람의 주관적 판단을 수치로 변환 |
| 복잡한 문제 해결 | AHP로 해결 불가능한 문제 대응 가능 |
다음은 ANP 한계이다.
| 한계 | 설명 |
|---|---|
| 계산 복잡도 높음 | 슈퍼매트릭스 구성과 수렴 계산이 복잡 |
| 주관적 오류 가능성 | 쌍대비교에서 편향 발생 가능 |
| 도구 의존도 높음 | 수작업보다는 전용 소프트웨어 사용 필요 (ex. Super Decisions) |
투자안 평가
투자안으로부터 예상되는 미래 현금흐름과 자본비용을 알고 있다고 가정할 때 각 투자안이 기업 가치 증가에 어느 정도 공헌하는지에 따라 투자안 경제성을 평가한다. 미래 현금 흐름을 고려 유무에 따라 전통적인 분석방법과 현금흐름할인법(DCF, discounted cash flow)으로 구분할 수 있다.
flowchart LR
subgraph " "
0[경제성 평가방법]
11[전통적 분석방법]
12[현금흐름할인방법]
21[원가비교법]
22[회수기간법]
23[회계적이익률법]
23["순현가법(NPV)"]
24["내부수익률법(IRR)"]
0 --- 11 & 12
11 --- 21 & 22 & 23
12 --- 23 & 24
end
전통적 분석방법
전통적 분석방법에는 회수기간법과 회계적 이익률법이 있다.
원가비교법
원가비교법(Minimum Cost Rule)은 최소비용법으로 대안을 선정하는 방법이다.
\[\text{Min\{각 투자안의 투자액과 비용의 합계\}} \tag{29.6}\]
회수기간법
회수기간법(payback period method)은 투자원금을 투자안을 통해 미래 현금유입으로부터 회수하는데 소요되는 기간을 산출하여 의사결정하는 방법이다.
\[ 회수기간 = \frac{투자액}{연간현금유입액} \tag{29.7}\]
의사결정 기준은 다음과 같다.
- 독립적 투자안
목표회수기간보다 짧은 투자안을 선택 - 상호배타적 투자안
목표회수기간보다 짧은 투자안들 중에서 회수기간이 가장 짧은 투자안 선택
회수기간법은 다음과 같은 장점과 단점을 갖는다.
| 장점 | 단점 |
|---|---|
| 계산이 간단하고 이해하기 쉬움 | 화폐의 시간적 가치를 무시 |
| 위험지표(risk indicator)로서 정보를 제공 (즉, 회수기간이 짧을수록 안전한 투자안으로 볼 수 있음) | 회수기간 이후 현금흐름이 무시됨 |
| 간접적으로 유동성 상태를 나타냄 (회수기간이 짧을수록 빠른 자금회수로 기업 유동성이 증가) | 회수기간만을 고려하기 때문에 투자안 수익성 자체가 무시됨 |
| 시설재의 내용수명 적정성을 평가하는 판단 기준으로 유용함 (특히, 수요변화나 기술진부화 등의 위험이 높은 경우) | 목표 회수기간을 결정하는 데 주관적임 |
| R&D 투자안과 같은 장기투자안일수록 부정적인 편의가 심함 | |
| 투자안에 따라 회수기간이 존재하지 않을 수 있음 | |
| 목표 회수기간 내에 회수되는 투자안이지만 NPV는 음(-)일 수 있음 |
할인회수기간법(discounted payback period method)은 미래 현금유입의 현재가치로부터 투자원금을 회수하는데 소요되는 기간으로 투자의사결정을 하는 방법이다. 화폐의 시간가치가 감안되어 있으나 회수기간 이후의 현금흐름이 무시된다는 단점이 여전히 존재한다.
회계적 이익률법
회계적 이익률(accounting rate of return)법은 장부가치기준으로 연평균투자액에 대한 연평균 회계적 순이익 비율을 구하여 투자결정을 하는 방법이다.
\[ 회계적 \ 이익률 = \frac{연평균순이익}{연평균투자액(장부가치)}, \ 또는 \ \frac{연평균순이익}{\frac{총투자액}{2}} \tag{29.8}\]
의사결정 기준은 다음과 같다. - 독립적 투자안
목표회계적 이익률(요구수익률)보다 높은 투자안을 선택 - 상호배타적인 투자안
목표회계적 이익률보다 높은 투자안들 중에서 목표 회계적 이익률이 가장 높은 투자안을 선택
회계적 이익률법은 다음과 같은 장단점을 갖는다.
| 장점 | 단점 |
|---|---|
| 계산이 간편하고 이해하기가 용이함 | 화폐의 시간가치를 무시함 |
| 회계자료를 바로 이용할 수 있어 편리함 | 회계처리방법에 따라 순이익이 달라지므로 객관성이 떨어짐 (예: 감가상각방법 차이) |
| 목표이익률 결정이 자의적임 |
현금흐름할인법
현금흐름할인법에는 순현가(NPV)법과 내부수익률(IRR)법이 있다.
순현가법
순현가법(NPV method)은 투자안과 관련된 현금 흐름은 편익에 해당되는 현금유입과 비용(투자액)에 해당되는 현금유출로 구분이 가능하다.
flowchart TB
01["현금흐름(CF, cash flow)"]
11["현금유입(CI, cash inflow)"]
12["현금유출(CO, cash outflow)"]
01 --- 11 & 12
순현가법은 순현재가치(NPV, net present value)를 근거로 투자안을 결정하는 방법이다. NPV는 투자로 인한 미래 기대현금유입을 적절한 할인율로 할인한 현재가치에서 투자액의 현재가치를 차감한 값을 의미한다.
계산식은 다음과 같다.
\[ NPV = 미래 \ 현금유입액 \ 현가 \ - \ 초기 \ 투자액 \]
\[ NPV = \sum^{n}_{t=1}\frac{CI_t}{(1+R)^t} - I_0 \tag{29.9}\]
여기서
- \(CI_t\) : \(t\)시점에서 예상되는 현금유입액
- \(I_0\) : 최초 투자액
- \(R\) : 할인율 또는 요구수익률(RRR, 자본비용)
의사결정 기준은 다음과 같다.
- 독립적 투자안: NPV > 0이면 채택
- 상호배타적 투자안: NPV > 0이고 NPV가 가장 큰 투자안을 채택
NPV법은 다음과 같은 특징을 갖는다.
- 화폐의 시간가치가 고려된 방법
- 오직 현금 흐름의 기대치와 자본비용만이 고려 (회계수치와는 무관)
- 모든 투자안의 NPV 합계는 바로 기업 가치
내부수익률법
내부수익률(IRR, internal rate of return)법은 기대 현금 유입 현가와 현금 유출 현가를 동일하게 하는 할인률인 IRR을 기준으로 투자를 결정하는 방식이다. 즉, 내부수익률(IRR)과 요구수익률(R)를 비교하여 투자를 결정한다. 계산법은 좌변에 이익현가를 두고 우변에 투자액 현가를 두어 일치시키는 할인율로 화폐의 시간가치가 감안된 예상투자수익률을 계산한다.
\[ \sum^{n}_{t=1}\frac{CI_t}{(1+IRR)^t} = \ I_0 \quad (여기서 \ 식을 \ 만족시키는 \ IRR \ 계산) \tag{29.10}\]
IRR은 현가표를 이용하여 시행착오법으로 구하며, 현가표에 정확한 값이 없을 경우 보간법 또는 재무계산기나 Excel을 이용하여 계산할 수도 있다.
의사결정 기준은 다음과 같다.
- 독리적인 투자안: IRR > R이면 채택
- 상호배타적 투자안: IRR > R이고 IRR이 제일 큰 투자안 채택
IRR법은 화폐의 시간가치가 감안된 평균투자수익률로 투자안을 평가한다는 특징이 있다.
문제해결방법
Pugh Matrix
Pugh Matrix는 여러 대안 중 최적의 선택을 하기 위해 각 대안을 기준에 따라 상대적으로 비교하는 방법이다. 기준 대안(Baseline Alternative)을 설정하고, 다른 대안들을 이에 비해 우수(+), 동등(0), 열등(-)으로 평가한다. 복잡한 수치 계산 없이 직관적으로 최적의 대안을 선정할 수 있다.
스마트폰 케이스 재료 선택을 예로 들면 다음과 같다.
- 목표: 가벼우면서도 내구성이 좋은 스마트폰 케이스 재료를 선정한다.
- 후보 재료
- 플라스틱
- 실리콘
- 알루미늄
- 탄소섬유
- 플라스틱
- 평가 기준
- 무게(가벼움)
- 내구성(충격 저항력)
- 비용(생산 비용)
- 가공 용이성(생산 공정 난이도)
- 무게(가벼움)
위 내용을 Pugh Matrix로 작성하면 다음과 같다.
| 평가 기준 | 플라스틱 | 실리콘 | 알루미늄 | 탄소섬유 |
|---|---|---|---|---|
| 무게 | 0 | - | - | + |
| 내구성 | - | 0 | + | ++ |
| 비용 | ++ | + | 0 | - |
| 가공 용이성 | + | ++ | - | 0 |
| 총계 | +1 | +1 | -1 | +1 |
- 기준 대안: 실리콘(0)
- 평가 방식:
- “+”: 기준 대안(실리콘)보다 우수하다.
- “0”: 기준 대안과 동등하다.
- “-”: 기준 대안보다 열등하다.
결과 분석 및 선택 방법은 다음과 같다.
- 탄소섬유, 플라스틱, 실리콘이 각각 +1로 가장 높은 평가를 받는다.
- 알루미늄은 가공이 어렵고 비용이 높아 총계가 -1로 나타난다.
- 최종적으로, 탄소섬유는 내구성이 매우 뛰어나며 무게도 가벼워 프리미엄 제품군에 적합하다.
- 비용 절감을 중시하는 경우에는 플라스틱을 선택한다.
Pugh Matrix 장점은 다음과 같다.
- 복잡한 계산이 필요 없고 직관적으로 이해하기 쉽다.
- 다양한 대안을 동시에 평가하고 비교할 수 있다.
- 팀 의사결정 과정에서 명확하고 투명한 선택을 돕는다.
Pugh Matrix는 재료 선택 과정에서 상대적 장단점을 명확하게 파악하고, 가장 적합한 재료를 선택하는 데 효과적인 방법이다.
Must-Want Matrix
Must-Want Matrix는 의사결정에서 필수 기준(Must)과 선호 기준(Want)을 구분해 대안을 평가하는 방법이다.
- Must 기준: 반드시 충족해야 하는 필수 조건
- Want 기준: 바람직하지만 필수가 아닌 선택적 조건
Must-Want 특징은 다음과 같다.
- Must 기준을 충족하지 못하는 대안은 바로 제외
- Want 기준은 점수화하여 대안 중 우선순위를 결정
노트북 외장재 선택을 사례로 들면 다음과 같다.
- 목표: 가벼우면서도 내구성이 높은 노트북 외장재 선정
- 대안: 알루미늄, 마그네슘 합금, 플라스틱, 탄소섬유
- Must 기준
- 내구성: 일정 수준 이상의 내구성 확보
- 열전도율: 과도한 발열 방지
- 내구성: 일정 수준 이상의 내구성 확보
- Want 기준:
- 무게: 노트북의 휴대성에 영향을 미치는 요소
- 비용: 생산 비용 절감
- 디자인: 외관의 세련미와 고급스러움
- 무게: 노트북의 휴대성에 영향을 미치는 요소
위 내용으로 Must-Want Matrix 작성하면 다음과 같다.
| 기준 | 알루미늄 | 마그네슘 합금 | 플라스틱 | 탄소섬유 |
|---|---|---|---|---|
| 내구성 (Must) | O | O | X | O |
| 열전도율 (Must) | O | O | O | O |
| 무게 (Want) | 3 | 4 | 5 | 4 |
| 비용 (Want) | 4 | 3 | 5 | 2 |
| 디자인 (Want) | 3 | 4 | 3 | 5 |
- 플라스틱은 내구성 기준(Must)을 충족하지 못해 제외됨.
- Want 기준을 점수화해 합산
- 알루미늄: 3 + 4 + 3 = 10점
- 마그네슘 합금: 4 + 3 + 4 = 11점
- 탄소섬유: 4 + 2 + 5 = 11점
- 알루미늄: 3 + 4 + 3 = 10점
평가 및 결론은 다음과 같이 정리할 수 있다.
- 마그네슘 합금과 탄소섬유가 같은 점수를 받았으나, 탄소섬유는 비용이 높은 단점이 있어 마그네슘 합금이 최종 선택됨.
- Must-Want Matrix를 통해 필수 기준을 충족하면서도 비용, 무게, 디자인에서 균형 잡힌 선택이 가능했음.
Must-Want Matrix 장점은 다음과 같다.
- 효율성: 불필요한 대안을 조기에 제거해 의사결정 속도 향상
- 명확성: 필수 조건과 선택 조건을 명확하게 구분해 객관적인 평가 가능
- 유연성: 다양한 제품 설계 및 재료 선택 과정에 적용 가능
제품 개발 초기 단계에서 Must-Want Matrix는 명확한 기준을 바탕으로 신속하고 합리적인 결정을 내리는 데 효과적인 도구이다.
TRIZ
TRIZ(Theory of Inventive Problem Solving)는 러시아의 발명가이자 엔지니어인 Genrich Altshuller가 개발한 창의적 문제해결 기법이다. TRIZ는 주로 기술적 문제를 해결하기 위한 방법론으로, 발명의 패턴과 원리를 분석하여 문제를 창의적으로 해결할 수 있는 체계적인 접근법을 제공한다. TRIZ의 핵심 아이디어는 발명의 혁신적인 해결책이 반복되는 문제 해결의 패턴에 따라 발전한다는 것이다.
TRIZ는 문제의 본질을 파악하고 해결책을 도출하기 위해 다양한 도구와 방법을 제공한다. 그 중 중요한 요소는 모순 해결, 발명적 원리, 기술 시스템의 진화와 관련된 이론들이다.
TRIZ 기법의 진행절차
TRIZ는 문제를 해결하는 체계적인 절차를 제공하며, 이를 통해 창의적인 아이디어를 생성할 수 있다. TRIZ의 주요 절차는 다음과 같다.
문제 정의
문제를 명확하게 정의하고, 해결하려는 기술적 문제나 개선점이 무엇인지 구체화한다. 이 단계에서는 문제의 본질과 원인을 파악하는 것이 중요하다.모순 분석
TRIZ에서는 기술적 문제를 해결할 때 모순을 분석하는 것이 핵심이다. 문제를 해결하려면 두 가지 상반되는 요구나 조건이 충돌하는 경우가 많다. TRIZ에서는 이러한 모순을 명확히 인식하고 해결 방법을 모색한다.- 물리적 모순: 두 상반되는 요구가 동시에 충족되어야 할 경우
- 기술적 모순: 문제 해결을 위한 조건이 서로 상충하는 경우
- 물리적 모순: 두 상반되는 요구가 동시에 충족되어야 할 경우
발명적 원리 적용
TRIZ는 40개의 발명적 원리를 제공한다. 이 원리들은 다양한 기술적 문제를 해결하기 위한 창의적인 아이디어를 도출하는 데 사용된다. 예를 들어, 분할 원리, 대체 원리, 반응 속도 조절 원리 등이 있다.자원 활용
TRIZ에서는 문제 해결에 필요한 자원을 재조합하거나 외부 자원을 활용하여 혁신적인 해결책을 찾는 방법도 제시한다. 이 단계에서는 문제 해결에 필요한 자원을 효율적으로 활용할 수 있는 방법을 모색한다.해결책 도출 및 검증
TRIZ에서 제시된 창의적인 해결책을 실제 문제에 적용해 보고, 그 유효성을 검증한다. 이 단계에서는 도출된 아이디어가 실제 문제를 효과적으로 해결하는지 평가하고 개선한다.
TRIZ 기법의 적용분야
TRIZ는 주로 기술적 문제를 해결하는 데 사용되지만, 그 적용 범위는 매우 넓다. 다음은 TRIZ 기법이 적용될 수 있는 주요 분야들이다.
기술 혁신 및 제품 개발
TRIZ는 제품의 성능을 개선하거나 새로운 제품을 개발하는 과정에서 창의적 문제 해결을 돕는다. 기술적 모순을 해결하고, 기존의 한계를 넘는 혁신적인 아이디어를 창출하는 데 유용하다.생산 공정 개선
제조업에서 생산성 향상, 비용 절감, 품질 개선을 위해 TRIZ를 활용할 수 있다. 생산 공정에서의 기술적 문제를 분석하고 효율적인 해결책을 제시할 수 있다.자동화 및 로봇 공학
TRIZ는 로봇 시스템과 자동화 기술의 문제를 해결하는 데도 활용된다. 기계적 모순을 해결하고, 로봇 시스템의 효율성을 높이는 방법을 제시한다.환경 문제 해결
환경 보호 및 자원 효율성을 높이기 위한 문제 해결에도 TRIZ가 적용될 수 있다. 예를 들어, 에너지 효율을 개선하거나 오염을 줄이는 방법을 찾는 데 유용하다.서비스 산업
기술적 문제뿐만 아니라 서비스 산업에서도 TRIZ는 유용하다. 서비스 프로세스의 개선, 고객 만족도를 높이기 위한 창의적인 해결책을 도출하는 데 사용할 수 있다.
TRIZ 기법은 창의적 문제 해결을 위한 강력한 도구로, 기술적 문제를 체계적으로 분석하고 해결책을 제시하는 데 매우 효과적이다. TRIZ는 발명의 원리와 문제 해결 패턴을 바탕으로 다양한 분야에서 적용할 수 있으며, 기업이나 조직에서 혁신적인 해결책을 찾는 데 큰 도움이 된다.
참고자료
FEA
FEA(Financial effect analyst)는 기업이나 조직 내에서 재무적인 영향을 분석하고 평가하는 전문가이다. 이 직무는 조직의 재무 상태와 성과를 평가하고, 중요한 재무 결정을 내리기 위한 정보를 제공하는 역할을 한다. 주로 재무제표, 투자 분석, 예산 계획, 비용 분석 등을 통해 기업의 재무 건전성을 높이고 효율적인 경영을 지원하는 역할을 한다.
FEA 주요 역할과 업무는 다음과 같다.
- 재무 분석
- 기업의 재무제표(손익계산서, 대차대조표 등)를 분석하여 회사의 재무 건강 상태를 평가한다.
- 수익성, 유동성, 재무 구조 등을 파악하여 조직의 재무 성과를 진단한다.
- 재무 계획 및 예산 수립
- 향후 예산을 수립하고, 예상되는 수익 및 비용을 분석하여 재무 목표를 설정한다.
- 각 부서별 예산을 조정하고, 조직의 재정적인 목표를 달성하기 위한 전략을 마련한다.
- 투자 분석
- 투자 프로젝트나 신사업에 대한 재무적 영향을 분석하여, 투자에 대한 수익성, 위험성 등을 평가한다.
- 기업의 자금을 어디에 투자할지 결정할 때, 재무적인 분석 결과를 바탕으로 전략적 결정을 지원한다.
- 비용 절감 및 효율성 향상
- 비용 구조를 분석하여 불필요한 비용을 식별하고, 이를 줄이기 위한 방안을 제시한다.
- 효율적인 자원 배분을 위해 재무적인 조정을 한다.
- 위험 관리
- 시장, 금융, 운영 등에서 발생할 수 있는 재무적 위험을 분석하고, 이를 관리하기 위한 전략을 개발한다.
- 환율 변동, 금리 변화, 채무 리스크 등과 같은 외부적인 요소를 고려하여 예측하고 대응한다.
- 보고서 작성 및 의사결정 지원
- 경영진이나 투자자들에게 재무 분석 결과를 보고서 형식으로 제공하여 의사결정을 돕는다.
- 분석을 통해 얻은 인사이트를 경영진에게 제공하여 전략적 결정을 내리도록 지원한다.
FEA로서 필요한 기술 및 자질은 다음과 같다.
- 재무 및 회계 지식: 재무제표, 회계 원칙, 투자 분석 등에 대한 깊은 이해가 필요하다.
- 분석적 사고: 데이터를 분석하고, 복잡한 문제를 해결하는 능력이 요구된다.
- 소프트웨어 활용 능력: Excel, ERP 시스템, 재무 분석 툴 등을 능숙하게 사용할 수 있어야 한다.
- 커뮤니케이션 능력: 분석 결과를 명확하고 효과적으로 전달할 수 있는 능력이 필요하다. 경영진과의 커뮤니케이션이 중요하다.
- 문제 해결 능력: 조직의 재무 상태를 개선하고, 비효율적인 부분을 찾아내는 문제 해결 능력이 중요하다.
- FEA 역할을 예로 들면 다음과 같다.
-
- 기업 합병 및 인수: 기업이 다른 회사를 인수하려는 경우, Financial Effect Analyst는 이 거래가 기업의 재무 상태에 미치는 영향을 분석하고, 리스크와 예상되는 수익성을 평가한다.
- 신규 프로젝트 투자: 회사가 새로운 프로젝트에 투자하려 할 때, 이 프로젝트가 기업 재무에 미치는 영향을 분석하여, 투자 여부를 결정하는 데 필요한 데이터를 제공한다.
- 예산 분석 및 조정: 각 부서의 예산이 초과되었을 때, 재무 분석가는 비용을 절감하기 위한 방안을 제시하고, 재무 목표에 맞게 예산을 재조정한다.
FEA는 기업 재무 상태와 성과를 평가하고 전략적 의사결정을 지원하는 중요한 역할을 한다. 이를 위해 재무 분석, 예산 수립, 투자 평가 등 다양한 재무 활동을 수행하며, 경영진이 합리적인 결정을 내릴 수 있도록 돕는다. 이 직무는 재무적인 통찰력을 제공하고 기업 성장과 효율성을 극대화하는 데 기여한다.
DEA
DEA(Data Envelopment Analysis)는 1978년 Charnes, Cooper, Rhodes에 의해 처음으로 제안되었으며, OR/M(Operations Research/Management, 운영과학/경영)에서 가장 널리 활용되는 방법 중 하나이다. 생산운영 관리와 경영과학분야에 있어 효율성을 측정하기 위해 사용되는 비모수적 방법이다. 주로 여러 개 투입(input)과 산출(output)을 가지는 동일한 유형의 의사결정단위(DMU, Deceision Making Unit) 간 상대적 효율성을 평가하는데 사용한다.
DEA 핵심개념은 다음과 같다.
- 의사결정단위(DMU): 병원, 학교, 공장, 점포 등 비교 대상이 되는 동일 유형 조직이나 부서
- 투입(input): 자원, 예산, 인력 등 DMU가 사용하는 것
- 산출(output): 제푸 수, 고객 만족도, 이익 등 DMU가 만들어 내는 결과
- 효율성(efficency): 산출/투입 비율로 계산되며, DEA는 이를 상대적 기준으로 평가함
DEA 주요 특징은 다음과 같다.
- 수학적 최적화 모델을 기반으로 한 평가 도구
- 비모수적 방법: 자료 분포나 함수 형태를 가정하지 않음
- 상대적 효율성 측정: 가장 효율적인 DMU를 기준으로 다른 단위 효율성을 평가
예를 들어 보면 다음과 같다.
- 5개 학교가 있고, 각 학교는 교사 수(투입)와 졸업생 수(산출)를 가지고 있다고 할 때, DEA는 가장 효율적으로 졸업생을 많이 배출한 학교를 기준으로 삼고, 다른 학교의 상대적 효율성을 계산
DEA 주요 활용 분야는 다음과 같다.
- 병원 간 서비스 효율 비교
- 공공기간 성과 분석
- 제조업체 생산성 비교
- 교육기간 운영 효율 분석
_EOD_
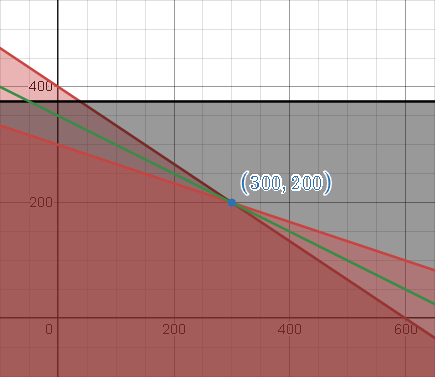
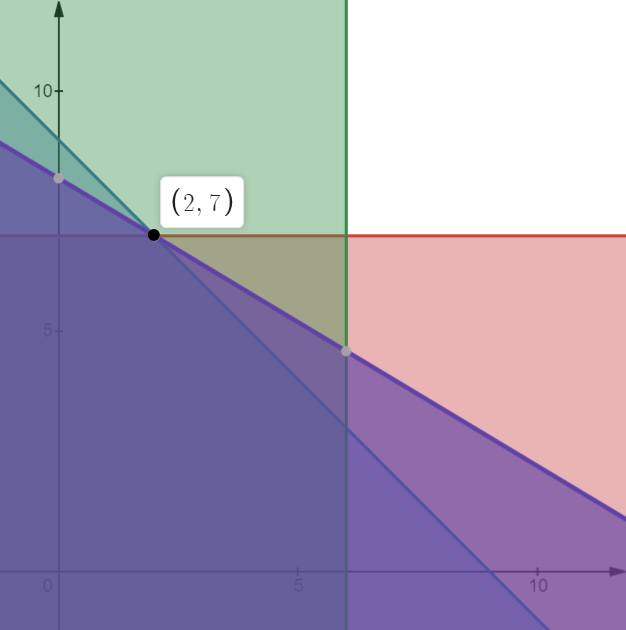 민감도 분석
민감도 분석